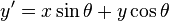A day or so ago I looked up the topic of using rotation matrices to modify the angle of a vector by an arbitrary amount. I visited none other than the WikiPedia page for rotation matrices.
The idea behind rotation matrices is to solve for the x and y coordinates after the rotation by using two separate equations. Here is a rotation matrix for 2 dimensions:
That matrix will rotate the 2D plane counterclockwise by angle θ. Using this knowledge, the new x and y coordinates for a point on a rotated vector would be solved for using these two equations:
Very simple! So here is an example problem: Say you have vector AB. AB = (2, 3).
To solve for a rotated counterclockwise version of this vector you input your desired angle of rotation in for θ, 2 for x and 3 for y. This rotation matrix rotates a 2D plane clockwise:
Rotation in 3 dimensions is basically the same process. All that is different is the z coordinate and modified rotation matrices. You simply solve for each individual coordinate with the rotation matrices for the z, x, and y axis. These three rotation matrices and more are found at the WikiPedia page for rotation matrices.
Thursday, May 13, 2010
Mini RPG
Today I worked on my Mini RPG. I added about 75 lines of code. I added a monster class, almost finished the battle function, modified and updated the main loop, and made some minor changes to the character class to allow for holding weapons and having hit points. I am really loving object orientation for this little program; things are super organized and simplified. I can't imagine creating this program without using any classes D:
I haven't had time to actually test the source file for bugs and errors, but I believe it is working.
Here is a link to my source: http://www.mediafire.com/download.php?mgmzmwnnwdg
I haven't had time to actually test the source file for bugs and errors, but I believe it is working.
Here is a link to my source: http://www.mediafire.com/download.php?mgmzmwnnwdg
Tuesday, May 11, 2010
Linear Algebra: Basics
Today with my math teacher I went over some of the basics of linear algebra. The two topics I went over included solving for the intersection of two lines in 3D space, and finding the angle between two vectors. The rest of the mathematical topics I'll try to cover in the near future include: finding a vector orthogonal to two other vectors in 3D space; finding the time T during the intersection of ray between a circle of sphere; using a matrix to rotate a vector by an arbitrary angle. I found these topics, as well as an entire survival guide for DigiPen students, at this site here. Hopefully by explaining the math I went over today I can solidify my own understanding.
First off: solving for the intersection of two lines in 3D space. I know how to do this in matrix form, as it is easiest and simplest in matrix form. Here is a matrix of the x y and z coordinates for a point in 3D space: [x, y, z]. An equation for a vector in 3D space consists of a point on a line, and the direction vector of a line multiplied by a magnitude. This magnitude represents the length of the line, whereas the timestep, or t, represents a constant.
Here is an equation for a line in 3D space: L1 = [2, 4, -1] + t[-1, 2, 3]. I just chose these numbers at random because they really don't matter. The first matrix is a point on the line. The second matrix is the rise, run, and the z equivalent to rise or run (just like two dimensional lines). You need a point on the line, otherwise the direction vector (rise//run//zrun) could sit anywhere in space. Without the direction vector for your line, you line could be facing in any direction as long as it sits on your point. The t is the magnitude of the direction vector, and these could be used as something to define the distance something traveled over time of t. t is just a constant.
In order to solve for the intersection of two lines, I'll quickly show the process with some variables. Here are the two lines: L1 = [a, b, c] + t[d, e, f]; L2 = [g, h, i] + r[j, k, l]. Now since these two equations each represent a line, the point of intersection is going to be a point that can be used to satisfy either of the equations. You just set both of the equations equal to each other, one variable at a time (x, y and z) and solve for each one. To solve for the x coordinate of the intersection you would use a + td = g + rj. You do this for variable a through c corresponding to d through f. Then using substitution, if need be, you can solve for t and then solve for the rest of the variables, thus getting a final matrix of [x, y, z].
The second thing I learned today was finding the angle between two vectors. Luckily, you only need the direction vectors of the line equations. This makes sense because no matter where the lines are in space, they will have the same angle of intersection as long as the direction of the lines face in stays constant. To do this, you use the equation of:
Theta, the zero thingy on the left, is the angle you are solving for. a and b both represent matrices that represent direction vectors, like the direction vectors in the line equations earlier in this post. Arccos is cos^-1. The a and b on the top half of the right side of the equation is pronounced as a dot b. The dot is the operator for the dot product. The dot product is used to find the scalar projection of a onto b, and vise versa. I honestly don't fully understand what exactly the dot product does yet (read last paragraph, I understand it now), but for now I just need it for equations like this one, and it returns a scalar value. To use the dot product on two 1x3 matrices, you would do this: [a, b, c] dot [d, e, f] = ((a x d) + (b x e) + (c x f). The |a| represents the magnitude of a, which is the length of a. If the direction vector of a line is representing velocity vectors, then the magnitude of a would be the speed of the direction vector. To find the magnitude of a 1x3 matrix you do this: |M| = |[a, b, c]| = sqrt(a^(2) + b^(2) + c^(2)). Does that look familiar? It should; it's basically the Pythagorean Theorem in 3D. It takes the rise, run, and zrun and converts the three into a length value, just like the Pythagorean Theorem does with two lines, except this is with three.
Now once you find a dot b, and magnitude of a times magnitude of b, you then divide a dot by magnitude of a times magnitude of b, then arccos that value which results in your angle!
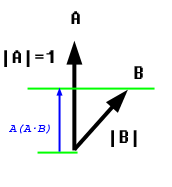
Dot product explained: Okay! I so I did a bit of research and asked a couple people some questions and now I understand what the value returned by the dot product does. It projects a vector onto another vector and returns the length. A dot B also equals B dot A, which makes sense because multiplication itself is commutative, and the formula for the dot product is just multiplication of three values. Here is a picture to help visualize this:
The blue line would be the dot product of A and B. This is very useful for collision in programming, and transforming vectors from one grid space to another. Here is a good example of using the dot product for 2D collision detection of convex polygons:
The red and blue are both one dimensional projections of the objects onto a line. The dotted line is perpendicular one side length of one of the objects. In the diagram is looks like it is perpendicular to both, which is fine, but it is important to understand that the dotted line is normal to one of the sides of one of the polygons. Once you find a dotted line that is perpendicular to a side of one of the shapes, you use the dot product on a two dimensional matrix and project both of the shapes onto the normal to the dotted line. You can then compare the two projections to see if they overlap. If the two projections overlap, you then try the entire process over for a different side of one of the polygons. Once you try this algorithm over each of the sides of each object and no collision vector was detected (a collision vector would be the length of overlap formed by overlapping projections) in at least one of the iterations, then the two objects are not colliding with one another.
Sources:
http://www.mvps.org/directx/articles/math/dot/index.htm
http://en.wikipedia.org/wiki/Dot_product
http://www.gamedev.net/reference/programming/features/verletPhys/page2.asp
First off: solving for the intersection of two lines in 3D space. I know how to do this in matrix form, as it is easiest and simplest in matrix form. Here is a matrix of the x y and z coordinates for a point in 3D space: [x, y, z]. An equation for a vector in 3D space consists of a point on a line, and the direction vector of a line multiplied by a magnitude. This magnitude represents the length of the line, whereas the timestep, or t, represents a constant.
Here is an equation for a line in 3D space: L1 = [2, 4, -1] + t[-1, 2, 3]. I just chose these numbers at random because they really don't matter. The first matrix is a point on the line. The second matrix is the rise, run, and the z equivalent to rise or run (just like two dimensional lines). You need a point on the line, otherwise the direction vector (rise//run//zrun) could sit anywhere in space. Without the direction vector for your line, you line could be facing in any direction as long as it sits on your point. The t is the magnitude of the direction vector, and these could be used as something to define the distance something traveled over time of t. t is just a constant.
In order to solve for the intersection of two lines, I'll quickly show the process with some variables. Here are the two lines: L1 = [a, b, c] + t[d, e, f]; L2 = [g, h, i] + r[j, k, l]. Now since these two equations each represent a line, the point of intersection is going to be a point that can be used to satisfy either of the equations. You just set both of the equations equal to each other, one variable at a time (x, y and z) and solve for each one. To solve for the x coordinate of the intersection you would use a + td = g + rj. You do this for variable a through c corresponding to d through f. Then using substitution, if need be, you can solve for t and then solve for the rest of the variables, thus getting a final matrix of [x, y, z].
The second thing I learned today was finding the angle between two vectors. Luckily, you only need the direction vectors of the line equations. This makes sense because no matter where the lines are in space, they will have the same angle of intersection as long as the direction of the lines face in stays constant. To do this, you use the equation of:
Theta, the zero thingy on the left, is the angle you are solving for. a and b both represent matrices that represent direction vectors, like the direction vectors in the line equations earlier in this post. Arccos is cos^-1. The a and b on the top half of the right side of the equation is pronounced as a dot b. The dot is the operator for the dot product. The dot product is used to find the scalar projection of a onto b, and vise versa. I honestly don't fully understand what exactly the dot product does yet (read last paragraph, I understand it now), but for now I just need it for equations like this one, and it returns a scalar value. To use the dot product on two 1x3 matrices, you would do this: [a, b, c] dot [d, e, f] = ((a x d) + (b x e) + (c x f). The |a| represents the magnitude of a, which is the length of a. If the direction vector of a line is representing velocity vectors, then the magnitude of a would be the speed of the direction vector. To find the magnitude of a 1x3 matrix you do this: |M| = |[a, b, c]| = sqrt(a^(2) + b^(2) + c^(2)). Does that look familiar? It should; it's basically the Pythagorean Theorem in 3D. It takes the rise, run, and zrun and converts the three into a length value, just like the Pythagorean Theorem does with two lines, except this is with three.
Now once you find a dot b, and magnitude of a times magnitude of b, you then divide a dot by magnitude of a times magnitude of b, then arccos that value which results in your angle!
Dot product explained: Okay! I so I did a bit of research and asked a couple people some questions and now I understand what the value returned by the dot product does. It projects a vector onto another vector and returns the length. A dot B also equals B dot A, which makes sense because multiplication itself is commutative, and the formula for the dot product is just multiplication of three values. Here is a picture to help visualize this:
The red and blue are both one dimensional projections of the objects onto a line. The dotted line is perpendicular one side length of one of the objects. In the diagram is looks like it is perpendicular to both, which is fine, but it is important to understand that the dotted line is normal to one of the sides of one of the polygons. Once you find a dotted line that is perpendicular to a side of one of the shapes, you use the dot product on a two dimensional matrix and project both of the shapes onto the normal to the dotted line. You can then compare the two projections to see if they overlap. If the two projections overlap, you then try the entire process over for a different side of one of the polygons. Once you try this algorithm over each of the sides of each object and no collision vector was detected (a collision vector would be the length of overlap formed by overlapping projections) in at least one of the iterations, then the two objects are not colliding with one another.
Sources:
http://www.mvps.org/directx/articles/math/dot/index.htm
http://en.wikipedia.org/wiki/Dot_product
http://www.gamedev.net/reference/programming/features/verletPhys/page2.asp
Monday, May 10, 2010
Game Design: Positive and Negative Feedback; Flow Control
As I've said a few times in the past, I have been reading Rules of Play: Game Design Fundamentals. Lately I have also been applying what I've learned into judging StarCraft mapping contests, like this one, and weaving them into my own map like this one. I've decided to take some of the knowledge and tools I've gained and write a post here about them. First, I want to talk about positive and negative feedback back loops in two different contexts.
The first context I want to talk about them in, is in the study of cybernetics.
The second meaning of positive and negative feedback would be rewards and punshiments to a player. Simply put, rewards are great to use to encourage players to make certain choices, and punishments are used to deter certain behavior. There is also a third category known as negative feedback. Negative feedback is not necessarily a punishment, but is used to deter a player from making specific choices. For example say you do not want your game to be focused on fighting, although you want to have an occasional enemy in your game. It turns out that too many players are focusing on finding and fighting enemies rather than experiencing your game how you designed it to be experienced. You do not want to punish the player as to deter them from playing at all, so what you could do instead is implement a clever negative feedback mechanism. You might be thinking that you could just make enemies stronger and therefore make the player want to avoid them -this might just make finding and killing enemies an interesting challenge for the player. Instead you could give the player absolutely no reward for killing the enemy (no points or anything), you could also make enemy encounters not worth the risk (as in making the player restart the level if an enemy kills them, or have enemies be "thieves" where if they hit you you lose items). If your goal is to make enemies something the player wants to avoid, give the player a reason to avoid them. If you find that fighting these enemies is truly fun for the players, you could also switch your game to a fighting one; it's your design, you decide.
As you can see, it can be hard to create a flow in gameplay for all different types of players. One way that game designers achieve balanced flow is to apply positive and/or negative feedback loops to a game's processes.
Here is an interesting excerpt from the book Rules of Play that talks about the design process for a game made by two designers:
The designers of this game implement two negative feedback loops. Did you see them? Onewould be the sneak attack ships. These ships react to the players being all alone at seas, and then appear out of nowhere to create an exciting experience. The other would be the water spout; the water spout reacts to the players entering the boundaries of the map, then spins them in the correct direction, thus keeping the game in a specific state. The guideships and weenies would be more a form of positive feedback in which encourage the player to make specific decisions. The guideships encourage the players to travel to the key focul points of the game while the weenies create enticing visual scenes that players are likely to travel to. Both of these provide the players with a reward and a reason to take specific actions.
The first context I want to talk about them in, is in the study of cybernetics.
Cybernetics deals with the ways a system gauges its effect and makes necessary adjustments. The simplest cybernetic device consists of a sensor, a comparator, and an activator. The sensor provides feedback to the comparator, which determines whether the machine is deviating from its established norm. The comparator then provides guidance to the activator, which produces an output that affects the environment in some way. This fundamental process of output-feedback-adjust-ment is the basis of cybernetics.—Stephen Littlejohn, Theories of Human Communication
As this quote explains, cybernetics is a study of how a system reacts and makes adjustments to the current state of the system. This should sound rather relevant to video games. This type of automated reaction is used all the time; have you ever played a game that automatically tiers to the user's level of skill? There are two primary types of adjustments that are made upon a system, these two are positive and negative feedback reactions, usually used within a loop.
For example, take a room with a thermostat and a heater. When this room's sensor, the thermostat, reads a certain temperature it can trigger the heater to react. This system can be rigged to perform a negative feedback reaction in which the heater heats the room when the temperature is less than or equal to a certain amount. Assuming the room naturally cools, the room's temperate will oscillate between a few degrees and stay that way, all the while the room's specific state is constantly changing. A positive feedback loop would be if the heater turns on when the temperate is equal to or greater than a specific temperature. In a positive feedback loop, the temperature of the room will spiral up and up once it hits a certain activation point. Both positive and negative feedback loops are essential tools to be used in game design.
Too often I see games designed in StarCraft maps that are too hard or too easy, or too hard or too easy once the player reaches a certain point. I also see games made in which the leader has no way of letting the other players catch up to him, because he has such a great advantage over the other players. I also see the losers in a game have no means of catching up to the leaders. What's the point of continuing play if the outcome of the match has already been determined in the middle of the game because the leading player has a tremendous advantage over the rest of the players? These types of design flaws can be controlled with positive and negative feedback loops. Usually positive feedback loops are harmful to a game's flow (flow will be explained more in depth soon), and should be switched out for negative feedback loops. If a leading player seems to be constantly destroying all the other players in an unfair way, create a negative feedback response in which the system (the game) reacts and hinders the leading player. Similarly, you can give advantages to the players in last place to encourage and help them catch up to the leaders.
A great example of a negative feedback response is in the game Super Mario Cart. In Super Mario Cart there are weapons you gain from running into question marked boxes with your cart. Once you hit one you obtain a random weapon. You have a much greater chance to obtain a powerful weapon when you are near last place in the race, and you have a much greater chance to obtain a weak weapon when you are in first place. This sort of automated reaction the system generates creates a much more compelling form of gameplay, in which all the racers are usually closely pitted against each other neck to neck until the very end of the race. This generates an exciting play in which the outcome of the overall match remains uncertain till the very end.
The second meaning of positive and negative feedback would be rewards and punshiments to a player. Simply put, rewards are great to use to encourage players to make certain choices, and punishments are used to deter certain behavior. There is also a third category known as negative feedback. Negative feedback is not necessarily a punishment, but is used to deter a player from making specific choices. For example say you do not want your game to be focused on fighting, although you want to have an occasional enemy in your game. It turns out that too many players are focusing on finding and fighting enemies rather than experiencing your game how you designed it to be experienced. You do not want to punish the player as to deter them from playing at all, so what you could do instead is implement a clever negative feedback mechanism. You might be thinking that you could just make enemies stronger and therefore make the player want to avoid them -this might just make finding and killing enemies an interesting challenge for the player. Instead you could give the player absolutely no reward for killing the enemy (no points or anything), you could also make enemy encounters not worth the risk (as in making the player restart the level if an enemy kills them, or have enemies be "thieves" where if they hit you you lose items). If your goal is to make enemies something the player wants to avoid, give the player a reason to avoid them. If you find that fighting these enemies is truly fun for the players, you could also switch your game to a fighting one; it's your design, you decide.
Flow; flow would be the fine balance between difficulty in a game and the player's skills. Skills do not just include physical coordination; skills also include knowledge of the game's workings, knowledge of the other player's skill level, physical coordination, intelligence level, and response time. There are more than likely many many more forms of skill which I did not mention, but these should give a general idea. The difficulty of the game is pretty self-explanatory. The flow channel of a game is a narrow isle where the difficulty of the game is perfectly balanced and matched to the skill level of the player. Here is a diagram of the flow channel graphed with challenge over skill level:
As you can see, it can be hard to create a flow in gameplay for all different types of players. One way that game designers achieve balanced flow is to apply positive and/or negative feedback loops to a game's processes.
Here is an interesting excerpt from the book Rules of Play that talks about the design process for a game made by two designers:
In a wonderful essay published on Gamasutra.com, Jesse Schell and Joe Shochet of Disney Imagineering write about the process of designing Pirates of the Caribbean-Battle for the Buccaneer Gold, a game "ride" where a group of players stands on a motion-platform pirate ship surrounded by video projections. During the game, one player steers the ship while the other players operate a number of cannons, firing at monsters, forts, and enemy vessels. Pirates of the Caribbean is designed as a condensed five-minute experience, and it was essential that players feel properly challenged at every moment of the game.In their design analysis, Schell and Shochet detail a number of design problems that had to be overcome in order to maximize player enjoyment. For example, during playtesting they identified as a problem the fact that the player steering the ship could take the ship to what they call "dull places," leading to a less engaging experience for all of the players. In the selected quotes below, Schell and Shochet outline some solutions to this problem:Architectural Weenies: "Weenie" is a phrase coined by Walt Disney himself. It refers to the technique used on movie sets of guiding stage dogs by holding up part of a sausage… In the case of Pirates, [there are] three main "weenies," one for each island: a volcano, an enormous fort, and a plume of smoke coming from a burning town. No matter which way the boat is facing, at least one of these "weenies" is in view. Since the coolest action takes place at the islands, [we wanted] to guide the captains to go there.Guide Ships: Since the short-term goal of the game is to fire on other pirate ships, captains strive to get near these ships so that their gunners can get a clear shot. Many of the ships in the Pirates world are "on their way" to the islands mentioned above. Many captains, in just trying to stay near these ships find that just as they have destroyed the ship, they have arrived at one of the islands, without even trying to get there.Sneak attacks: What if the captain ignores the guide ships? Even if he heads toward one of the "weenies" it might mean as long as a minute during which the gunners have little to shoot at. For this reason, [we] created special "sneak attack" ships that "magically" appear behind the players' ship, and quickly pull up alongside, when no other boats are in range.The Waterspout: This was [a] nickname for [a] "last ditch" forcefield that surrounds the game play area.If a captain tries to sail out of the main game play area and out to open sea, they hit the forcefield, and the ship is "magically" pointed back to where the action is. The few guests who see this don't even realize that anything unusual has happened. They are just pleased to have their boat going somewhere cool.Schell and Shochet are thinking in very experiential terms, using clever techniques to subtly guide player action in meaningful directions. At the time of its release, Pirates was a very high-tech production, featuring real-time 3D graphics, physically engaging cannon-firing interfaces, and a large motion platform to simulate a pirate ship rocking on the waves. Often in these instances, a desire to "properly" simulate a coherent 3D space or "correctly" output logical behavior for computer-controlled characters overshadows the design of the actual play experience. But Schell and Shochet had no hesitation in making pirate ships "magically" appear to guide the player, or abandoning "realistic" physics to have the player's ship turn on a dime to facilitate navigation. As they put it,"By choosing to be less concerned with reality and more concerned with what was fun, we created an experience that…is easier to adapt to, quicker to learn, and is a better show." In game design, player experience should always trump so-called "realism."
Boredom and anxiety, as game design watchwords, are wonderful because they speak directly to player experience. As you shape and sculpt your players' pleasure, you are guiding them between the Scylla and Charybdis of anxiety and boredom.This task is made all the more difficult because, as we know, the experience of play can only be indirectly designed. How do you create a set of rules that maximizes the play of pleasure for your audience?
The designers of this game implement two negative feedback loops. Did you see them? Onewould be the sneak attack ships. These ships react to the players being all alone at seas, and then appear out of nowhere to create an exciting experience. The other would be the water spout; the water spout reacts to the players entering the boundaries of the map, then spins them in the correct direction, thus keeping the game in a specific state. The guideships and weenies would be more a form of positive feedback in which encourage the player to make specific decisions. The guideships encourage the players to travel to the key focul points of the game while the weenies create enticing visual scenes that players are likely to travel to. Both of these provide the players with a reward and a reason to take specific actions.
Wednesday, May 5, 2010
Mini RPG: Continued
I have been working on a StarCraft map for a week long contest at StarEdit.net, however, today I forgot to bring my flashdrive with me so I now have no access to my mapfile and cannot work on it. Since I am unable to work on that for most of today, I decided to work on this file since I can copy//paste the source from my older post :)
Today I added in some comments to my code for easier read, added in a tiny method for the character class to add inventory items to the inventory (which is just a single list within the character class), created an item class, and started on the function that handles battles.
Overall progress is going at a decent pace while working on this project, but, I am not spending much time on it currently due to the week long contest I had mentioned.
At the moment this file doesn't do anything new, but has new code within it.
Here is my current source file: http://www.mediafire.com/?ymwminmhige
Today I added in some comments to my code for easier read, added in a tiny method for the character class to add inventory items to the inventory (which is just a single list within the character class), created an item class, and started on the function that handles battles.
Overall progress is going at a decent pace while working on this project, but, I am not spending much time on it currently due to the week long contest I had mentioned.
At the moment this file doesn't do anything new, but has new code within it.
Here is my current source file: http://www.mediafire.com/?ymwminmhige
Subscribe to:
Comments (Atom)