A day or so ago I looked up the topic of using rotation matrices to modify the angle of a vector by an arbitrary amount. I visited none other than the WikiPedia page for rotation matrices.
The idea behind rotation matrices is to solve for the x and y coordinates after the rotation by using two separate equations. Here is a rotation matrix for 2 dimensions:
That matrix will rotate the 2D plane counterclockwise by angle θ. Using this knowledge, the new x and y coordinates for a point on a rotated vector would be solved for using these two equations:
Very simple! So here is an example problem: Say you have vector AB. AB = (2, 3).
To solve for a rotated counterclockwise version of this vector you input your desired angle of rotation in for θ, 2 for x and 3 for y. This rotation matrix rotates a 2D plane clockwise:
Rotation in 3 dimensions is basically the same process. All that is different is the z coordinate and modified rotation matrices. You simply solve for each individual coordinate with the rotation matrices for the z, x, and y axis. These three rotation matrices and more are found at the WikiPedia page for rotation matrices.
Thursday, May 13, 2010
Subscribe to:
Post Comments (Atom)


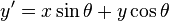





No comments:
Post a Comment
Note: Only a member of this blog may post a comment.